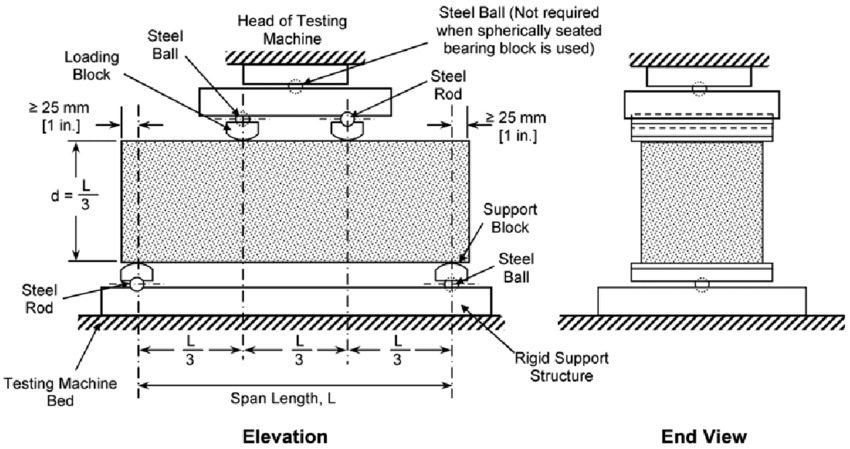
The modulus of rupture is a critical mechanical property used to measure the strength and resistance of a material to breaking or fracturing under bending or flexural stress. It is commonly used in engineering and construction to assess the structural integrity of various materials, including concrete, wood, ceramics, and composites. Understanding the modulus of rupture formula and its application is essential for engineers, designers, and material scientists. In this comprehensive guide, we will explore the modulus of rupture formula, its significance, the variables involved, and how to calculate and interpret the results accurately.
The Modulus of Rupture Formula The modulus of rupture is calculated using the following formula:
Modulus of Rupture = Maximum Bending Moment / Section Modulus
The maximum bending moment is the maximum stress experienced by the material when subjected to a bending load. It represents the critical point at which the material may fracture. The section modulus refers to the geometrical property of the cross-section of the material, which determines its resistance to bending.
Variables and Units (150 words): The variables in the modulus of rupture formula include:
- Maximum Bending Moment: Typically measured in force multiplied by distance (e.g., N-m or lb-ft).
- Section Modulus: Measured in length cubed (e.g., m^3 or ft^3).
Calculation and Interpretation
To calculate the modulus of rupture, you need to determine the maximum bending moment and the section modulus. The bending moment can calculate using structural analysis methods or obtained through experimental testing. The section modulus depends on the shape and dimensions of the cross-section and can obtain from engineering handbooks or by performing calculations specific to the material and its geometry.
Once the maximum bending moment and section modulus known you can use the modulus of rupture formula to calculate the value. The resulting value represents the maximum stress that the material can withstand before fracturing under bending stress.
Interpreting the modulus of rupture value is crucial in determining the material’s suitability for specific applications. A higher modulus of rupture indicates greater strength and resistance to bending, while a lower value suggests a material’s vulnerability to fracture. The modulus of rupture value can compare against design requirements, industry standards. Or specifications to assess whether the material meets the necessary strength criteria.
Factors Affecting Modulus of Rupture:
Several factors can influence the modulus of rupture, including material composition, manufacturing processes, moisture content, temperature, and loading conditions. Different materials have varying inherent strengths and fracture properties, which directly affect their modulus of rupture. Additionally, factors such as defects, microstructure, and structural arrangement within the material can impact its resistance to bending stress.
Conclusion:
Understanding the modulus of rupture formula and its significance is crucial for assessing. The strength and fracture behavior of materials under bending stress. By accurately calculating and interpreting the modulus of rupture, engineers and material scientists can make informed. Decisions regarding material selection, design optimization, and structural integrity assessments.